整備士や検査員のテスト問題の答え合わせに使いやすいように、ブレーキ制動力を自動車分解整備記録簿の形に類似させた計算フォームを作りました。
分解整備記録簿は指定工場で車検を受けるともらえます。※参考:安い指定車検工場
その記録簿には制動力の測定結果が表示されているので、このページでご自身の車の制動距離をシミュレーションしてみて下さい。
重さや路面状況で変化する制動距離を視覚的にとらえる事ができるので制動力をイメージしやすいです。
制動力の計算だけでなく、制動時間や制動距離を求める計算式と計算フォームもあるので、お気軽にご利用して下さい。
目次
ブレーキ制動力の計算式
車検で記録簿に記載する制動力の計算は簡単です。
- 前制動力(N)÷前軸重(kg)=前制動力(N/kg)
- 後制動力(N)÷前軸重(kg)=後制動力(N/kg)
- 合計制動力÷合計軸重=合計制動力(N/kg)
- 前左右差制動力÷前軸重=前左右差制動力(N/kg)
- 後左右差制動力÷後軸重=後左右差制動力(N/kg)
- 駐車ブレーキ制動力÷合計軸重=駐車ブレーキ制動力(N/kg)
車検で計算するのは以上です。この計算フォームが下にあるので、利用してみて下さい。
これは車検で測定する制動力ですが、実際の走行テストで測定する制動力は違います。
車検ではタイヤの下にローラーを置き、ローラーをモーターで回転させ、抵抗力を測定します。
その抵抗力が制動力に計算されて表示します。
停車状態で検査するので、慣性力による荷重移動がなく、空気抵抗も関わらないので、最低基準の測定だと思って下さい。
制動力計算シート 車検記録簿用
下の白枠内に数値を入れると計算された数値がグレー枠に出力されます。
パソコン画面で見ると車検記録簿と似たような配置で表示されるので見やすいと思います。
※軸重は車検証に記載されているので測定しなくてもわかりますが、各車輪の制動力は車検のブレーキテスターで測定しなければわかりません。
制動力の保安基準4.9N/kgとは？
車検の制動力検査において制動性能は4.9N/kg以上必要です。
力(N)はFなのでF=ma成り立ちます。
mは質量、aは加速度なので、Fはkg×m/s^2とも表せます。
F=Nなので、Nにkg×m/s^2を代入すると4.9N/kg=4.9×kg×m/s^2÷kgと置き換える事が出来て、4.9m/s^2になります。
ですので、4.9N/kgは4.9m/s^2の減速度が必要という事になります。
そして力を表す場合、力はm×aなので、重量900kgですと、4.9N/kg×900kg=4410N以上が全体の制動力になります。
この4410Nは900kgの車を4.9m/s^2で減速させるのに必要な力です。ですので、9.3m/s^2の急ブレーキで停車させるには9.3×900=8370Nが必要だということになります。
次は国土交通省のブレーキ性能試験を元に、通常は実測しなければわからない制動力をシミュレーションで求めてみます。
制動力シミュレーション
ダイハツ ムーヴを例に制動力を出してみます。
上のページの停止距離は時速100km/hでブレーキを踏んだ結果です。ムーヴの停止距離は41.4mになっています。
ですので下記計算フォームには停車距離41.4を入力し、速度は100と入力して計算ボタンを押すと停車までにかかった時間と減速度が出ます。
減速度が9.3m/s^2になったと思います。
上のムーヴの重量は840kgと書かれています。
車の計算では1人の重量を55kgとするので、停車試験では1人乗車の895kgとなります。
計算を簡単したいので、ここでは総重量900kgにします。
制動力Fの公式は「F=ma」です。
Fが制動力、mが質量、aが加速度なので、F=900×9.3になり、F=8370Nがムーヴの制動力です。
実際に車を停車させる場合、前後の荷重が変わります。
車に乗られている方ならわかりますが、ブレーキを踏むと車は前に沈むので、前輪に大きな荷重がかかり、慣性力で後輪は軽くなります。
慣性力は車の傾きにも関係します。
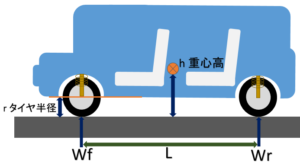
重心が高いと傾きやすいので、前後の制動力を出すには重心高も計算します。
車の重心高は一般公開されていないので「車の重心高を計算」ページで計算して下のフォームに入力すると減速度に合った前後の最大制動力が出ます。
$$ Bf+Br=ma=F $$
ブレーキ時の荷重変化分$$ \Delta W=\frac{mah}{L} $$
前後の制動力の関係$$ \frac{Br}{Bf}= \frac{Wr-\Delta W}{Wf+\Delta W}=C$$
計算過程$$ F= Bf+Br $$
$$ F=Bf+(C×Bf) $$
$$ F=Bf(C+1) $$
荷重変化後の前後制動力$$ Bf=\frac{F}{C+1} Br=F-Bf $$
上の計算式を下のフォームで実行します。
減速度0.15m/s^2は一般道路で不快なく普通に停車できるソフトなブレーキ操作です。
3.0m/s^2ですと助手席に置いてある荷物が落ちる位ですので、軽い急ブレーキです。
5.0m/s^2以上ですと助手席の人はダッシュボードを手で抑えたくなるような急ブレーキです。
9.0m/s^2以上はタイヤがロックし、事故が発生する可能性があるほどの急ブレーキです。
上で算出された制動力でシミュレーションしてみます。
加速度も試したい方は駆動力の計算ページも参考に見て下さい。
155/65R14のタイヤ半径は0.279mですが、シミュレーションでこのサイズですと小さくてタイヤの回転加速と回転ロックが見えないので、タイヤ半径を0.35mに設定しました。
制動力、車両重量、道路状態などをカスタマイズして制動力試験と同じ時速100kmからフルブレーキをかけて停車して制動距離を見て下さい。
テスト車両の初期設定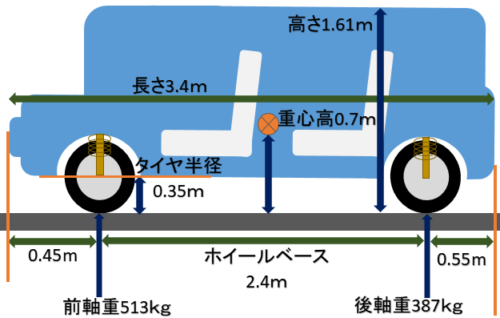
| 前制動力 | 6700N | 後制動力 | 1674N | |
| 車両重量 | 1000kg | 駆動力 | 5000N | |
| ホイールベース | 2.4m | 重心高 | 0.7m | |
| 前輪軸重 | 513kg | 後輪軸重 | 387kg |
初期設定はムーヴのデータに合わせてあります。重心高は車両重量100kg増えると約0.14ｍ下がります。
※最高速度を上げると加速度も上がります。最高速度300km以上、駆動力20000Ｎ以上にすると車がジャンプしたり回転します。上手に車体の浮き沈みをコント―ロールしたり回転しながらテストしてみるのも面白いと思います。車体は軽自動車設定なので、総重量は1500kgが限界です。
どうでしたか？実際は時速100kmでの制動距離は100m前後と言われています。
実際は様々な影響によってテストより制動性能が下がると思った方がよさそうです。
ブレーキの異常は、車検で最も重要なチェック項目の一つです。
物理計算で理想的な状態を理解しても、実際の車の状態はどうでしょうか？
安心してドライブするためにも、プロによる点検・整備が欠かせません。
あなたの車の状態をプロに診断してもらいませんか？ [車検どこがいい？安くて安心車検店をご紹介]
制動距離の計算式
以下3つの式で停止距離を計算できます。
$$ L=\frac{vt}{2}= \frac{v^2}{2a}= \frac{v^2}{2μg} $$
- L: 距離「ブレーキを踏んでから停車まで」
- V: 速度「ブレーキを踏んだ時」
- t: 時間「ブレーキを踏んでから停車まで」
- a: 加速度「ブレーキを踏んでから停車まで」
- μ: タイヤと路面の摩擦係数「0.2～0.9」
- g: 重力加速度「9.8」
- m: 車両質量「kg」
- B: ブレーキトルク「Nm」
以下に3つの式の計算フォームを作りました。
制動時間と速度で制動距離を計算
v-tグラフの面積が移動距離になります。
三角形の面積は速度の変化分と時間をかけて2で割ります。
$$ L=\frac{vt}{2} $$
※時速(km/h)を3.6で割って秒速(m/s)に変換してから計算しています。 |
加速度と速度で制動距離を計算
速度と加速度の関係はv=atなので、下の式のように変化させる事ができます。
$$ L=\frac{vt}{2} の tに \frac{v}{a}を代入 $$
$$ L= \frac{v^2}{2a} $$
速度と摩擦係数と重力で制動距離を計算
力学的エネルギーで考えるとブレーキの仕事と運動エネルギーは等しいです。
$$ 仕事W=運動エネルギーK $$
ブレーキトルクBは次のような抵抗の式で表せます。
$$ B=μmg $$
μは摩擦、mは車両重量、gは重力です。
ブレーキトルクに距離をかけるとブレーキの仕事になります。
$$ W=BL $$
運動エネルギーは次の式です。
$$ K=\frac{1}{2}mv^2 $$
よって2つの式を合わせると
$$ BL= \frac{1}{2}mv^2 → μmgL=\frac{1}{2} mv^2$$
になります。ここから距離Lを求める為に右辺にμmgを持っていくと
$$ L= \frac{v^2}{2μg} $$
になります。この式になるまで質量、タイヤと道路の摩擦抵抗、重力加速度が入るので、この計算は上の2つより現実的な結果になります。
ここに出てきた摩擦係数は以下2つに影響されます。
- タイヤの性能と状態
- 路面の種類と状態
ここではタイヤの性能は標準状態の一般的なタイヤで考えるので、計算式に入れません。
路面だけ計算式に入れます。
$$ L= \frac{v^2}{2μg} $$
以上が制動力、制動時間、制動距離の計算です。
こちらで安い車検店を紹介しています。
上の指定車検工場で車検を受けて制動力の記録簿をもらってテストしてみて下さい。
ブレーキトラブルや、その他の修理費用に悩まされているのであれば、それは愛車の買い替えを検討する良いタイミングかもしれません。
最新の車は制動力も上がって、より快適で安全な走行が可能です。
今の愛車の価値を調べてみませんか？ [損しない車の売却方法]
シミュレーション入力用の計算式
上の制動力シミュレーションはPlanck.jsで作りました。
ここからはシミュレーションの設定に使う計算と数値です。
自分が使いやすように設置したものなので、皆さんはここから下は必要ないと思います。
プログラムに入力する数値
- 車両重量 900ｋｇ
- 乗車定員2人 110ｋｇ
- 最大積載量 350ｋｇ
- 総重量 1360kg
- 車両重量内訳 車体780kg ばね下重量30kg/1本
- 最高速度 100ｋｍ/ｈ 80rad/s
- タイヤ半径 0.35ｍ
- 最大トルク 1800Nm
- 駆動力(タイヤ半径で割る) 1200/0.35＝5143N
- ブレーキトルク※ F：1000Nm R：544Nm
- ブレーキ力(タイヤ半径で割る) F：2857N R：1553N
※車検の制動力の最低基準が4.9N/kg×重量なので、4.9N/kg×900kg=4410Nでトルクは1544Nmです。
一般的に前輪ブレーキトルクは後輪の2倍なので1000Nmにします。
そうしますとリヤは544Nmになります。
しかし、これは最低基準の制動トルクなので、実際にこの力では制動距離が長すぎてしまいます。
角速度の計算式rad/s
Planck.jsでは速度を角速度で表します。
車のメーターは時速で標準されているので、Planck. jsで扱うには時速から角速度に変換する必要があります。
$$ ω= \frac{v}{r} $$
車体密度の計算式kg/m^2
ここのシミュレーションは2次元ですので、密度はkm/m^2になります。
このプログラムでは車のサイズによって変化する質量に対応するために車の面密度を入力してサイズと計算しています。
$$ ρ_c= \frac{M}{S} $$
タイヤ密度の計算式kg/m^2
普通乗用車は4輪タイヤですが、このシミュレーションは2次元で真横から見ているので、タイヤは2本しかありません。
2本を4本分として質量計算してあります。
$$ ρ_T= \frac{WT}{TS} $$
